Gaining confidence in synthetic control causal inference with sensitivity analysis
April 05, 2023 Published by Ciarán Gilligan-Lee, Thanos Vlontzos
Introduction
Understanding cause and effect relationships in Spotify data to inform decision-making is crucial for best serving Spotify’s users and the company. The generally-accepted gold standard solution to this problem is to conduct a randomised controlled trial, or A/B test. However, in many situations such trials cannot be performed; they could be unethical, exorbitantly expensive, or technologically infeasible. In the absence of such trials, many methods have been developed to infer the causal impact of an intervention or treatment from observational data given certain assumptions. One of the most widely used causal inference approaches in economics, marketing, and medicine are synthetic control methods.
To concretely illustrate synthetic controls, consider the launch of an advertising campaign in a specific geographic region, aimed to increase sales of a product there. To estimate the impact of this campaign, the synthetic control method uses the number of sales of the product in different regions, where no policy change was implemented, to build a model which predicts the pre-campaign sales in the campaign region. This model is then used to predict product sales in the campaign region in the counterfactual world where no advertising campaign was launched. By comparing the model prediction to actual sales in that region after the campaign was launched, one can estimate its impact.
In the standard synthetic control set-up, the model is taken to be a weighted, linear combination of sales in the no-campaign regions. To train the model, one needs to determine the weights for sales in each no-campaign region that minimise the error when predicting the sales in the campaign region before the campaign was launched. The linearity of the model is justified by assuming an underlying linear factor model for all regions, or units, that is the same for all time periods, both before and after the intervention. Recent work has removed the need for the linear factor model assumption and proven identifiability from a non-parametric assumption: that units are aggregates of smaller units. This assumption is reasonable in situations like our advertising campaign example, where total sales in a region is just the aggregate of sales from each individual in that region. However, in many applications, this assumption does not apply. In medicine for instance, patients are not generally considered to be aggregates of smaller units. When the aggregate unit assumption cannot be justified, can the causal effect of an intervention on a specific unit be identified from data about “similar” units not impacted by the intervention?
Returning to our example, the reason sales in different regions provide good synthetic control candidates is that the causes of sales in most regions are very similar, consisting of demographic factors, socioeconomic status of residents, and so on. Informally, sales in “similar” regions act as proxies for these, generally unobserved, causes of sales in the campaign region. That is, before the campaign, the causes of sales in the campaign region are also causes of sales in the no-campaign region—they are common causes of the campaign and no-campaign regions. This relationship between the target variable and synthetic control candidates is illustrated as a directed acyclic graph, or DAG, in the below Figure. Previous work combined this formulation with results from the proximal causal inference literature to prove one can identify the causal effect of an intervention on the target unit from data about the proxy units not impacted by the intervention. Hence, in our example, observing sales in multiple no-campaign regions allows one to predict the contemporaneous evolution of sales in the campaign region in the absence of the campaign without needing any linearity assumptions.
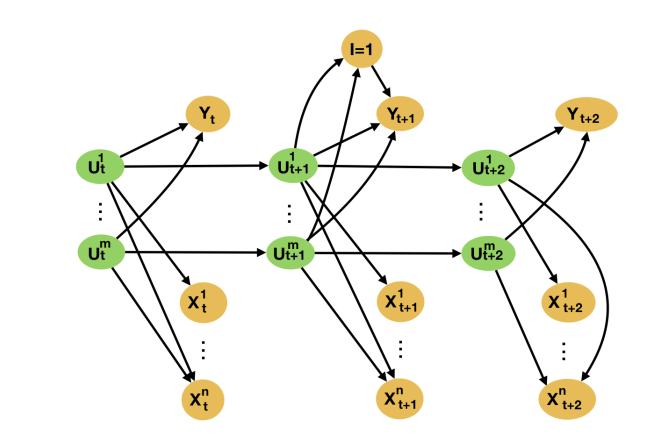
However, in all previous identifiability proofs, it is implicitly assumed that the underlying assumptions are satisfied for all time periods, both pre- and post-intervention. This is a strong assumption, as models can only be learned in the pre-intervention period. That is, one of the main assumptions underlying the validity of synthetic control models is that there is no unobserved heterogeneity in the relationship between the target and the control time-series observed in the pre-intervention period. Such unobserved heterogeneity could, for instance, be due to unaccounted-for causes of the target unit.
In our paper we addressed this challenge, and proved identifiability can be obtained without the need for the requirement that assumptions hold for all time periods before and after the intervention, by proving it follows from the principle of invariant causal mechanisms. Moreover, for the first time, we formulate and study synthetic control models in Pearl’s structural causal model framework.
Sensitivity analysis
As the assumptions underlying our identifiability proof cannot be empirically tested—as with all causal inference results—it is vital to conduct a formal sensitivity analysis to determine robustness of the causal estimate to violations of these assumptions. In propensity-based causal inference for instance, sensitivity analysis has been conducted to determine how robust propensity-based causal estimates are to the presence of unobserved confounders. These sensitivity analyses derived a relationship between the influence of unobserved confounders and the resulting bias in causal effect estimation. This understanding allows one to bound bias in causal effect estimation as a function of unobserved confounder influence. From this a domain expert can offer judgments of the bias due to plausible levels of unobserved confounding.
However, despite the importance of this problem—and the wide use of synthetic control methods in many disciplines—general methods for sensitivity analysis of synthetic control methods are under-studied. Our paper remedied this discrepancy and provided a general framework for sensitivity analysis of synthetic control causal inference to violations of the assumptions underlying our nonparametric identifiability proof.
Bounding the potential bias
One of the main assumptions of our identifiability proof is that the DAG from the introduction is satisfied. But this can be violated if there is an underlying latent, and proxy thereof, that we have not been able to include in our analysis. Such a situation is graphically illustrated in the below DAG. Our aim is to bound the bias that such a situation could lead to.
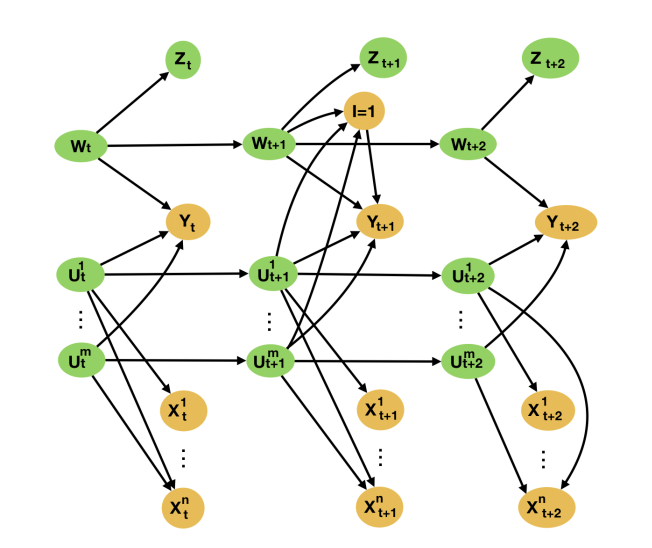
As with all sensitivity analyses, the bound we derive in our paper on the bias is in terms of latent quantities. As such, an analyst will need to make plausibility judgments in order to devise a bound in terms of observable quantities. Indeed, if an analyst believes they have not missed latent causes as important to our problem as the ones they included proxies for, then we can upper bound the bias in the worst case by taking the maximums in the above bound on the bias to be the maximums in the observed.
To test our bound, we assessed its validity on a series of synthetic and real world data. Using simulations, we investigate our bound in a valid and invalid setting. Moreover, we test on well known open source datasets used frequently in synthetic control papers to demonstrate the bound in a real world setting.
Conclusion
One of the most widely used causal inference approaches are synthetic control methods. However, in all previous identifiability proofs, it is implicitly assumed that the underlying assumptions are satisfied for all time periods both pre- and post-intervention. This is a strong assumption, as models can only be learned in the pre-intervention period. Our paper addressed this challenge, and proved identifiability without the need for this assumption by showing it follows from the principle of invariant causal mechanisms. Moreover, for the first time, we formulated and studied synthetic control models in Pearl’s structural causal model framework.
Importantly, we provided a general framework for sensitivity analysis of synthetic control models to violations of the assumptions underlying nonparametric identifiability. We concluded by providing an empirical demonstration of our sensitivity analysis approach on real-world data.
For full details, see our paper
Non-parametric identifiability and sensitivity analysis of synthetic control models
Jakob Zeitler, Athanasios Vlontzos, & Ciarán M. Gilligan-Lee
CLeaR (Causal Learning and Reasoning), 2023
