Estimating long-term outcome of algorithms

May 09, 2024 Published by Yuta Saito, Himan Abdollahpouri, Jesse Anderton. Ben Carterette, Mounia Lalmas

Summary

There are numerous scenarios where the short- and long-term consequences of an algorithm can differ. To estimate these long-term effects, one could conduct extensive online experiments, but these may require months to yield the desired insights, thus slowing down the process of selecting the right algorithm. In this work, we introduce a statistical approach that allows for the offline evaluation of an algorithm’s long-term outcomes by using only historical and short-term experimental data.

Estimating long-term outcomes

Often, we would like to know the long-term consequences, such as a specific metric of interest several months after applying a new algorithm, of algorithmic changes. Intuitively, the most accurate way of doing this is to run an online experiment, or A/B test, of the new algorithm for a sufficiently long period and measure its effectiveness. However, this procedure of running a new algorithm for a long time has several clear downsides:

• Decision-making of algorithm selection would become extremely slow. For example, if we run a year-long online experiment, we never know what algorithm would work best for a full one year.
• Running an experiment to test a new algorithm for a long time can be risky, since the new algorithm might be detrimental to the users’ experience.

Thus, having robust statistical methods to estimate the long-term outcomes of an algorithm without conducting extensive A/B testing would be highly advantageous.

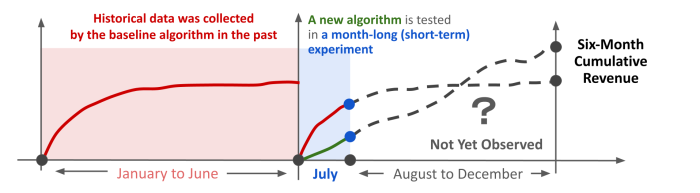
The figure above illustrates a hypothetical scenario where a baseline algorithm operated until June, generating historical data. In July, a short-term online experiment started to compare this baseline with a new algorithm. By the end of July, the baseline algorithm outperformed the new algorithm based on the chosen metric. However, projections suggest that by year-end, the new algorithm would surpass the baseline, a trend not apparent at the conclusion of the short-term experiment. This work aims to predict these long-term outcomes using the available data.

Existing Approaches

At a high-level, there are two existing approaches to estimate the long-term outcome of algorithms without actually conducting long-term experiments, namely long-term causal inference (long-term CI) and typical Off-policy evaluation (typical OPE).

Long-term causal inference: A conventional approach to estimating the long-term outcome of algorithmic changes is through a method known as long-term causal inference (LCI). LCI aims to achieve this by using historical data to infer the causal relationship between short-term surrogate outcomes (such as clicks, likes) and long-term outcomes (such as user retention a year from now). For this to be valid, LCI necessitates an assumption known as surrogacy. This requires that the short-term outcomes hold sufficient information to identify the distribution of the long-term outcome. However, this assumption has been considered restrictive and challenging to satisfy because it demands the presence of sufficient short-term surrogates that enable perfect identification of the long-term outcome. In other words, the connection between short-term and long-term outcomes must remain entirely consistent across all algorithms. Figure below demonstrates LCI assumption regarding surrogacy and ignoring action effects which could vary for different algorithms to estimate long-term rewards. 

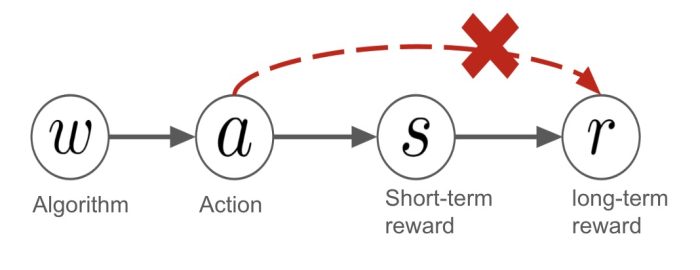
Overall, in LCI, the assumption is that surrogacy fully explains long-term rewards.
In other words, LCI estimates long-term reward by only leveraging surrogate effects. 
Long-term reward ≅  surrogate effect 

Off-policy evaluation: To estimate the long-term outcome without the restrictive surrogacy assumption, one could potentially apply off-policy evaluation (OPE) techniques such as Inverse Propensity Scoring (IPS) and Doubly-Robust (DR) methods, to historical data. Unlike LCI, OPE employs action choice probabilities under new and baseline algorithms, eliminating the need for surrogacy. However, typical OPE methods cannot take advantage of short-term rewards, which could be very beneficial as weaker yet less noisy signals particularly when the long-term reward is noisy. 

The Proposed Method (Long-term Off-policy Evaluation or LOPE)

To overcome the limitations of both LCI and OPE methods, we introduce a new method named Long-term Off-Policy Evaluation (LOPE). LOPE is a new OPE problem where we aim to estimate the long-term outcome of a new policy, but we can use short-term rewards and short-term experiment data in addition to historical data. To solve this new statistical estimation problem efficiently, we develop a new estimator based on a decomposition of the expected long-term reward function into surrogate and action effects. The surrogate effect is a component of the long-term reward explained by the observable short-term rewards, while the action effect is the residual term that cannot be captured solely by the short-term surrogates and is also influenced by the specific choice of actions or items. The surrogacy assumption of LCI can be viewed as a special case of this reward function decomposition since surrogacy is an assumption that completely ignores the action effect.  Therefore, LOPE is a more general formulation than LCI. 

In contrast, in our proposed approach (LOPE), long-term reward is a combination of surrogate and action effects. 

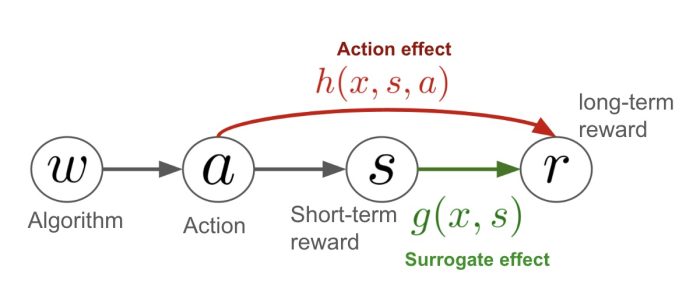
 Long-term reward ≅  surrogate effect  +  action effect

On top of the decomposition, our new estimator estimates the surrogate effect via importance weights defined using short-term rewards. The action effect is then addressed via a reward regression akin to LCI. Intuitively, LOPE is better than typical OPE methods because it can leverage the short-term rewards effectively to estimate the surrogate effect, leading to substantial variance reduction when the long-term reward is noisy. LOPE is also better than LCI, simply because it does not ignore the action effect as LCI does via assuming surrogacy. 

The benefits of LOPE are as follows:

• LOPE can fully utilize short-term outcomes in the historical data and short-term experiment result, which results in a lower variance estimator than typical OPE particularly when the long-term outcome is sparse and noisy.
• LOPE does not assume surrogacy like long-term CI, so our method is more robust to the violation of such an unverifiable assumption.
• LOPE can produce a new learning algorithm specifically designed to optimize long-term outcomes, a task unachievable with long-term CI. This approach is anticipated to outperform methods derived from conventional OPE, thanks to its strategic use of short-term results.

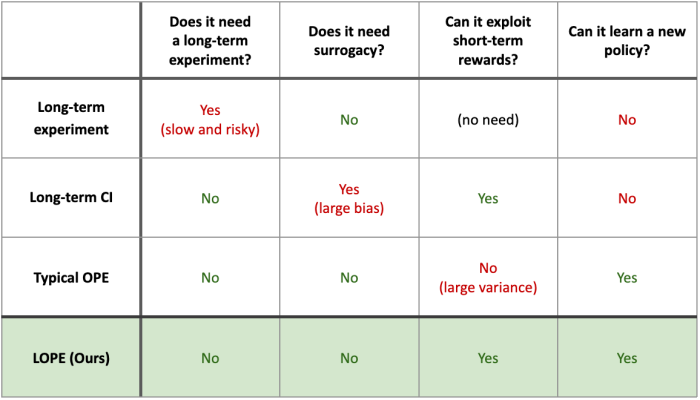
The following table summarizes the comparison of LOPE against these existing baselines. “Long-term experiment” refers to the infeasible “skyline” method (since it is intuitively the most accurate) of actually running a long-term online experiment of the baseline and new algorithms.

Results

We evaluated LOPE using simulation. Simulation is a powerful and commonly used way of evaluating the accuracy of offline evaluation methods. It is especially beneficial to compare various methods across different scenarios, such as noise levels or when certain assumptions are violated, and to thoroughly evaluate our method from multiple perspectives before confidently applying it to real data.

We evaluated the four mentioned approaches—Long-term Experiment, Long-term CI, Typical OPE, and LOPE (comprising a total of five methods, as typical OPE includes two versions)—using the following metrics for offline evaluation and selection:

• MSE (lower the better): accuracy of estimating the performance (expected long-term outcome) of the new model using only historical and short-term experiment data.
• Squared Bias (lower the better): the first component of MSE and measures the difference between the ground-truth performance of a model and the expected value of each estimator. This metric is useful to see the properties of estimators.
• Variance (lower the better): the second component of MSE and measures how stable each estimator is. This metric is useful to see the properties of estimators.

The following figure shows the metrics relative to those of the skyline (long-term experiment) with varying historical data sizes using simulation.

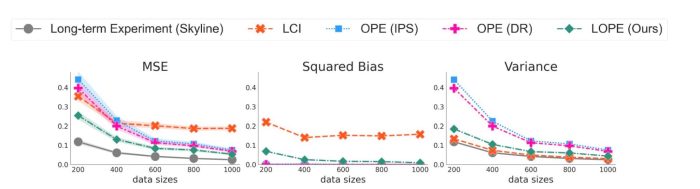
These plots show the estimators’ accuracy regarding long-term value estimation when we vary the size of the historical and short-term experiment data from 200 to 1,000 to compare how sample-efficient each method is. We observe that LOPE provides the lowest MSE among the feasible methods in all cases. LOPE is substantially better than the OPE methods, particularly when the data size is small (LOPE achieves a 36% reduction in MSE from DR when n=200). This is because LOPE produces substantially lower variance by effectively combining short-term rewards and long-term reward while the OPE methods use only the latter, which is very noisy. In addition, LOPE performs much better than LCI, particularly when the data size is large (LOPE achieves 71% reduction in MSE from LCI when n=1,000), since LOPE has much lower bias. The substantial bias of LCI even with large data sizes is due to its inability to deal with the violation of surrogacy.

We also experimented with varying degrees of noise in long-term reward and also varying levels of surrogacy violation to test the robustness of different methods.. LOPE showed overall best results under various degrees of noise. Regarding different levels of surrogacy violation, LOPE also performed more robustly. We also tested LOPE to estimate the long-term outcome of several real-world A/B tests at Spotify. LOPE consistently provided more accurate estimation. 

For more details about the results please read the full paper:
Long-term Off-Policy Evaluation and Learning
Yuta Saito, Himan Abdollahpouri, Jesse Anderton, Ben Carterette, and Mounia Lalmas.
The Web Conference, 2024