Model Selection for Production System via Automated Online Experiments

Machine learning practitioners regularly have to select the best model to deploy in production. At Spotify, for instance, we might develop a set of candidate recommender systems that each suggest a slightly different personalized playlist to a user and select the best one for production. Selecting the system that suggests the most satisfying playlists or tracks is not an easy task, as the machine learning model is only an intermediate component of the whole system.
We tackle this issue in a recent NeurIPS 2020 paper, where we propose an automated online experimentation (AOE) mechanism that can efficiently select the best model from a large pool of models, while only performing a few online experiments. Our approach (summarized in Figure 1 below) relies on a Bayesian surrogate model of the immediate user feedback, which is then used to compute predictions of the real online metric, e.g. click-through rate, frequency of track completion, etc. These predictions are used to rank different models by means of acquisition functions, which trade off exploration and exploitation. The model with the highest score is then deployed in production, yielding real data gathered from users, which is used to update the Bayesian surrogate model. We can repeat this process until convergence or until the experiment budget is exhausted.
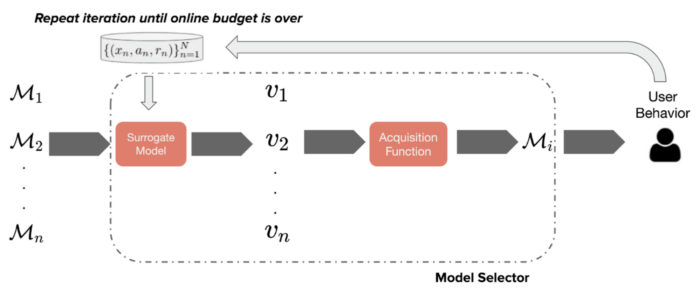
Fig. 1: Schematic that describes model selection via automated online experiments.
The model selection problem
We wish to select the best model from a pool of models, which may, for instance, correspond to different types of recommender systems or models trained with different hyper-parameters. Because the machine learning aspect of these models is only a part of the whole system, classical model selection methods, such as cross-validation, do not capture the actual downstream performance well. Instead, randomized online experiments, such as A/B tests, are often used in practice, as they provide a direct measure of the whole system performance. Unfortunately, they are relatively inefficient and may lead to potentially bad systems being deployed.
In comparison, our AOE approach considers data collection as part of the model selection process and selects the best model via iterative online experiments. The downstream performance of a particular model is measured by an accumulative metric, which we define to be an expectation of the immediate feedback received from the user. This could, for instance, correspond to whether or not a user has completed or liked a particular recommended track. Below we discuss how to estimate the accumulative metric and how to select the next model to deploy in the online experiments.
Bayesian surrogate model
We wish to maximize the accumulative metric, which is an expectation of immediate feedback. The distribution of the immediate feedback, however, is generally unknown, and we model it using a Gaussian Process (GP) surrogate model. Importantly, the distribution of immediate feedback, as well as the GP, only takes user decisions and user features as input, not the candidate model. This means that no matter which model is deployed to gather real data, we can always use that data to update the GP surrogate model. Updating the GP is generally expensive for the large quantity of data points obtained via online experiments, which is why we use variational sparse GP approximations for inference.
Using the GP surrogate model of the distribution of immediate feedback, we can then compute downstream predictions of the accumulative metric for each model in the candidate set. After making a few structural assumptions, we can also derive a distribution over this predicted accumulative metric: this can be done analytically for data with Gaussian noise, and via sampling otherwise. With this, we can essentially compute uncertainties in the predicted accumulative metrics, which allows us to efficiently trade-off exploring the candidate set and exploiting well-performing models.
Choosing the next online experiment
We use an acquisition function to guide the choice of the next online experiment. These effectively trade off maximizing the GP mean and minimizing the GP variance, commonly referred to as an exploration-exploitation trade-off. We consider popular acquisition functions from the Bayesian Optimization (BO) literature: expected improvement (EI), probability of improvement (PI) and upper confidence bound (UCB). These can be used out-of-the-box with the distribution over the predicted accumulative metric.
A major difference of our method to regular BO approaches is that the space of choices, i.e. the set of candidate models, is no longer the same as the input space of the surrogate model, e.g. user decisions and user features. On one hand, this means that some popular acquisition functions, such as entropy search (ES), cannot be used with our AOE method. On the other hand, this means that we can define a surrogate model over the space of decisions and features, which is generally a structured domain. The set of candidate models might, however, be a highly unstructured space, which makes it difficult to define a surrogate model over it.
Experimental results
For reproducibility, we construct simulators based on real data that can be used to generate estimates of the real online metric. We demonstrate the performance of AOE in two experiments, where the machine learning models are support vector machines (SVMs) and recommender systems.
In our first experiment, we construct a simulator on a classification dataset (the “letter” dataset from the UCI repository), where the set of candidate models are the SVMs with different choices of the two tuning parameters. The accumulative metric in this case is simply the average accuracy on a hold-out test set. For this classification experiment, we can visualize the surface of estimated accumulative metrics from all of the candidate models, over the two-dimensional space defined by the two tuning parameters of a SVM. This is shown in Figure 2 below for AOE and other baselines, after 20 iterations of sequentially gathering data. Clearly, AOE provides a metric surface that is visually consistent with the ground-truth and outperforms all other baseline approaches. From such a metric surface, we can select the best performing model.
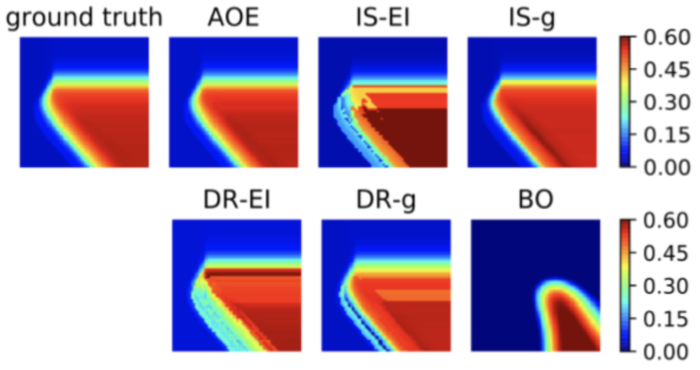
Fig. 2: Heatmaps of the estimated accumulative metric for the ground-truth, AOE and other baselines.
In our second experiment, we perform model selection for recommender systems, with a simulator constructed using the MovieLens 100k dataset. In this setting, a recommender system takes a user ID as input and returns an item ID for recommendation; the performance is then measured by the average response rate.
Figure 3 shows the (average) performance of AOE and other baselines as a function of online iterations. The left plot shows that AOE always identifies the true best model after the first iteration, unlike the other baselines. The right plot shows that AOE also has a consistently lower root-mean-square error (RMSE) of the estimated metric to the true metric. Note that the Bayesian Optimization (BO) baseline is unable to reduce RMSE because it does not have the prior knowledge that the accumulative metric (the average response rate) ranges between zero and one.
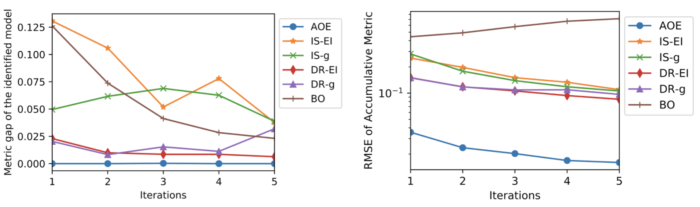
Fig. 3: Results for the recommender system experiments, for AOE and other baselines. The left plot shows the metric gap between the identified and true optimal model, the right plot shows the RMSE to the optimal accumulative metric.
Conclusions
Model selection for production systems does not fit into the classical model selection paradigm. We rectify this by proposing a new method, called AOE, that takes data collection into the model selection process, selecting the best model via iterative online experiments. Compared to other popular approaches such as A/B testing, our method allows for selection from a much larger pool of candidates and outperforms off-policy evaluation by actively reducing selection bias.
More information about the methodology, experiments and related work can be found in our paper:
Model Selection for Production System via Automated Online Experiments. Zhenwen Dai, Praveen Ravichandran, Ghazal Fazelnia, Ben Carterette and Mounia Lalmas.NeurIPS 2020.
Steven Kleinegesse is a PhD student at The University of Edinburgh, and is currently on a summer internship at Spotify.



