Can we correctly attribute changes among many possible causes when unobserved confounders are present?

What can we do when we cannot do an A/B test?
There are many A/B tests we might like to run, but which are too technically challenging, risky in terms of user impact or even impossible to perform. For instance, in the classic example of whether smoking causes lung cancer, forcing a randomly selected group of people to smoke is unethical if we believe it might damage their health. In the context of technology companies, if we want to understand if app crashes cause users to churn, we would have to randomly select a subgroup of users and crash their apps on purpose – not something we would want to consider given we do not want to break their trust.
With no prospect of testing and a clear risk of misleading results from observational data, what are we to do? Good answers to these questions could inform decision-making in many ways, helping us understand what type of content we should promote to attain the best business outcomes, or how we should prioritise app changes and fixes, and so on. Fortunately the causal inference toolkit can provide actionable answers about cause and effect from observational data like these (and assumptions that must be carefully scrutinised for each application).
In the applications we have discussed thus far, only a single intervention is possible at a given time, or interventions are applied one after another in a sequential manner. However, in some important areas, multiple interventions are concurrently applied. For instance, in medicine, patients that possess many comorbidities may have to be simultaneously treated with multiple prescriptions; in computational advertising, people may be targeted by multiple concurrent campaigns; and in dietetics, the nutritional content of meals can be considered a joint intervention from which we wish to learn the effects of individual nutritional components. Moreover, during the pandemic, many interventions were applied at the same time, such as mask wearing, working from home, closure of schools, and so on.
How can we learn the impact of individual interventions from such joint interventional data? This is the question we addressed in our paper.
Disentangling the impacts of multiple, interacting treatments
Disentangling the effects of single interventions from jointly applied interventions is a challenging task–especially as simultaneously applied interventions can interact, leading to consequences not seen when considering single interventions separately. This problem is made harder still by the possible presence of unobserved confounders, which influence both treatments and outcome. Our paper addresses this challenge, by aiming to learn the effect of a single-intervention from both observational data and jointly applied sets of interventions.
Formalising the problem
Identifiability is a fundamental concept in parametric statistics that relates to the quantities that can, or can not, be learned from data. An estimand is said to be identifiable from specific types of data if it is theoretically possible to learn this estimand, given infinite samples from the data.
If two causal models coincide on said data then they must coincide on the value of the estimand in question. Hence if one finds two causal models which agree on said data, but disagree on the estimand, then the estimand is not identifiable unless further restrictions are imposed.
Formally, the question we address is this: Given samples from the data regimes that induce
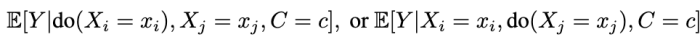
when can we learn the conditional average effects of single interventions, shown below?
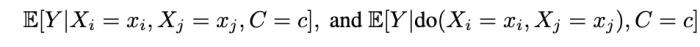
We prove that this is not generally possible. That is, without restrictions on the causal model, single-intervention effects cannot be identified from observations and joint-interventions.
However, we do provide identification proofs demonstrating it can be achieved in certain classes of non-linear continuous causal models with additive multivariate Gaussian noise–even in the presence of unobserved confounders. This reasonably weak additive noise assumption is prevalent in the causal inference and discovery literature. Importantly, we show how to incorporate observed covariates, which can be high-dimensional, and hence learn heterogeneous treatment effects for single-interventions.

The formal statement of our main result.
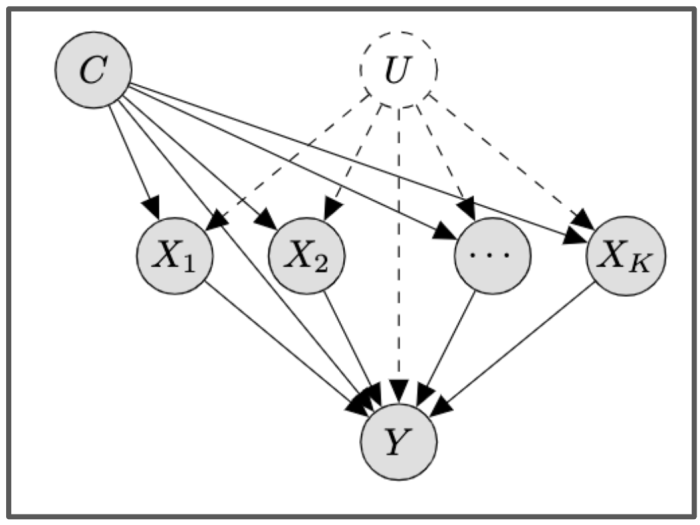
The causal structure we prove identifiability for. The X’s are the different treatments, C represents the observed confounders, and U the unobserved confounders. The X’s can interact in a possibly non-linear manner to give rise to the outcome, Y.
Estimation algorithm and empirical validation
In addition to proving theoretically that causal disentanglement is possible given our assumptions, our paper also provides an algorithm to learn the parameters of the proposed causal model and disentangle single interventions from joint interventions. Experimenting on synthetic data, we showed this algorithm can accurately estimate unseen sets of interventions.
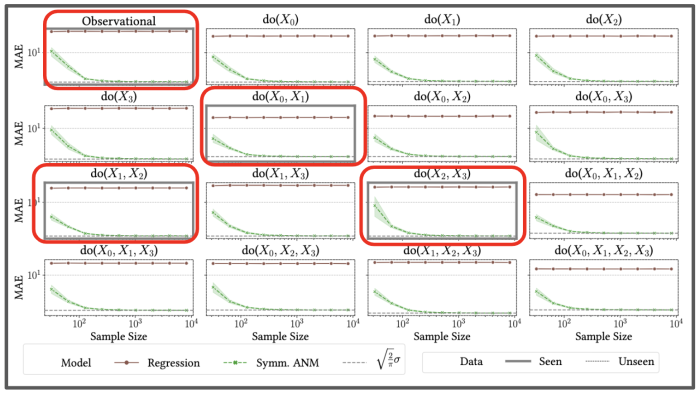
We provided our algorithm with data from joint interventions highlighted in the red boxes, and showed empirically it could accurately predict the impact of single, and other joint interventions it had never seen before.
We also showed that our method is consistent under varying levels of unobserved confounding by testing it on semi-synthetic setup on real-world data from the International Stroke Trial database. This was a large, randomised trial of up to 14 days of antithrombotic therapy after stroke onset. There are two possible treatments: the aspirin allocation dosage, and the heparin allocation dosage. The goal is to understand the effects of these treatments on a composite outcome, a continuous value in [0,1] predicting the likelihood of patients’ recovery.
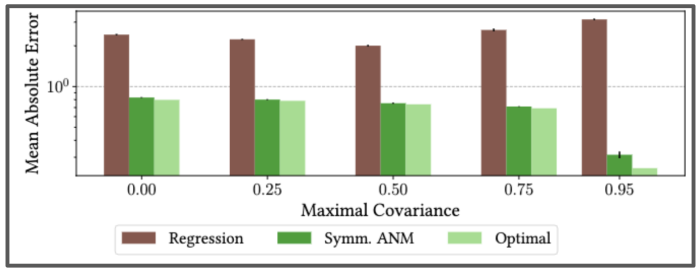
Using real data from the International Stroke Trial, and adding in synthetic unobserved confounding, we find our algorithm can correctly learn the full causal model–even as the strength of unobserved confounding increases.
Conclusion
Our work was motivated by the need for methods that can disentangle the effects of single interventions from jointly applied interventions. As multiple interventions can interact in possibly complex ways, this is a challenging task; even more so in the presence of unobserved confounders. The first result of our paper was a proof that such disentanglement is not possible in the general setting, even when we restrict the influence of the unobserved confounders to be additive in nature. Our main result however, was to provide a proof of identifiability in the reasonable additive noise model setting. Additionally, we showed how to incorporate observed covariates, and have empirically demonstrated our method. For more information about paper:
Disentangling Causal Effects from Sets of Interventions in the Presence of Unobserved Confounders Olivier Jeunen, Ciarán M. Gilligan-Lee, Rishabh Mehrotra and Mounia Lalmas NeurIPS 2022



