Answering counterfactual “what-if” questions in a trustworthy and efficient manner

Introduction
Answering causal questions with machine learning algorithms is a challenging yet critical task. While it is easy to spot correlation, unravelling causation necessitates careful examination of confounding variables and experimental design.
At Spotify, identifying the causal impact of recommending a specific type of content on a user can be challenging due to potential omitted variable bias. For instance, a user could love music, which means they spend more time using Spotify than others. This increases the likelihood they will see a certain recommendation, but also increases the likelihood they will continually engage with Spotify regardless. Answering this question properly requires advanced statistical methods and a thorough understanding of the underlying causal mechanisms to determine the true effect of our recommendations. And that is not all. We are also on a quest to discover what it truly means to be a fan. We are digging deep into the potential causes of fandom and analysing the causal effect of a user's actions. Our mission at Spotify is to understand the complex relationship between our recommendations and user engagement.
While in the above examples, the treatment in question was binary—recommending specific content or not—given the large amount of music, podcasts and audiobook content we have access to, we need to move beyond just quantifying the impact of binary treatments.
In this work, we take a step forward, leaving the well-researched binary treatment and outcome scenarios to delve into the world of categorical variables. We propose and evaluate a new paradigm in answering counterfactual queries using deep neural networks. Our methodology is evaluated in a wide range of publicly available datasets from Epidemiology, Medicine, and explainability in Finance—showcasing the real world applicability of our work.
Interventions vs Counterfactuals
While recent machine learning advances have enabled certain causal questions to be answered in high-dimensional datasets, most of these methods focus on Interventions, which only constitute the second level of Pearl’s three-level causal hierarchy. Judea Pearl's ladder of causality explains that interventions are at a higher level of causality than observations or associations, and they enable us to test the effects of actions. At the top of the hierarchy sit Counterfactuals. These subsume interventions and allow one to assign fully causal explanations to data. Counterfactuals investigate alternative outcomes, by asking what would have happened had some of the initial conditions been different. The crucial difference between counterfactuals and interventions is that the evidence the counterfactual is “counter-to” can contain the variables we wish to intervene on or predict.
One explicit example of a counterfactual question is the following: “Given that an artist released a specific track and it was streamed a certain amount, what would have happened had they released a different track?” Here we can use the observation of how well the original track was received to update our knowledge about how engaged that audience is, and use that knowledge to better predict the impact of an alternate track. A corresponding interventional query would be “what is the impact of releasing a single on the growth of my audience?”. Here, the evidence that the audience has grown is not used in estimating the impact. By utilising this additional information, counterfactuals enable more nuanced and personalised reasoning and decision making.
Non-Identifiability
Picture this: you have a powerful machine learning model that can predict the effects of interventions and guide your decision making, you are quite excited to see it in action. But wait, is it always reliable? Unfortunately, the answer is not always clear-cut. The problem lies in the non-identifiability of counterfactuals, which means that even if your model is trained on observations and interventions, its predictions can sometimes clash with domain knowledge. This can be a major roadblock, as we want our models to accurately reflect reality. As the models agree on the data they’re trained on, we must impose extra constraints to learn the model that generates domain-trustworthy counterfactuals.
Let us look at an illustrative example from the field of epidemiology, formalised by the following Directed Acyclic Graph (DAG) and accompanying equations, below. In the context of epidemiology, X is the presence of a risk factor and Y is the presence of a disease. From epidemiological domain knowledge, it is believed that risk factors always increase the likelihood that a disease is present—referred to as “no-prevention”, that no individual in the population can be helped by exposure to the risk factor. Hence, if one observes a disease, but not the risk factor, then, in that context, if we had intervened to give that individual the risk factor, the likelihood of them not having the disease must be zero—as having the risk factor can only increase the likelihood of a disease
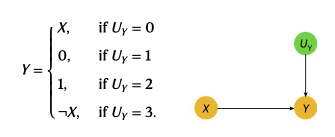
Under this regime, two potential probability distributions for the latent variable U_y are
P(UY=0) = 1/2, P(UY=1) = 1/6, P(UY=2) 1/6, and P(UY=3) = 1/6
and
P(UY=0) = 1/3, P(UY=1) = 1/3, P(UY=2) 1/3, and P(UY=3) = 0.
These two distributions can give the same observations and interventions but differ on their counterfactual estimations. By definition counterfactuals are not observable so we cannot know a priori which one is the correct answer. However, the first example clashes with the epidemiology domain knowledge mentioned above, as we outline in our paper.
This is where identifiability comes into the picture. Identifiability constraints offer theoretical guarantees that in the situations where they are fulfilled the answer to counterfactual questions are identifiable and unique from observational data. In our example that X and Y are binary variables it is enough to enforce a monotonicity constraint as this perfectly captures the epidemiological domain knowledge. The model that satisfies the constraint is the one with probability distribution:
P(UY=0) = 1/3, P(UY=1) = 1/3, P(UY=2) 1/3, and P(UY=3) = 0.
Counterfactual Ordering
But what happens when we have multiple categories of treatment and outcomes? In these cases we can only offer a partial identifiability constraint. In other words, only in the cases where our derived constraint is satisfied can we eliminate counterfactuals that disagree with our domain knowledge and intuition but cannot uniquely identify the answer. Despite this shortcoming we show in practice that this constraint can eliminate enough non-intuitive answers to make practical applications have good performance.
We name our partial-identifiability constraint Counterfactual Ordering and it encodes the following intuition: If intervention X only increases the likelihood of outcome Y relative to any other intervention, without increasing the likelihood of another outcome, then intervention X must increase the likelihood that the outcome we observe is at least as high as Y, regardless of the context.
From an engineering perspective, Counterfactual Ordering implies a set of constraints on the causal model. In our paper we prove that these are in fact equivalent to monotonicity, which can be enforced during causal model training to ensure the learned model satisfies counterfactual ordering.
Deep Twin Networks
Having derived a constraint that would enable partial-identification of our counterfactual queries from observational data we are left with the task to learn a model that follows said constraints and produces reliable results from real-world data. For this we introduce deep twin networks.
These are deep neural networks that, when trained, are capable of twin network counterfactual inference—an alternative to the abduction, action, & prediction method of counterfactual inference. Twin networks were introduced by Balke and Pearl in 1994 and reduce estimating counterfactuals to performing Bayesian inference on a larger causal model, known as a twin network, where the factual and counterfactual worlds are jointly graphically represented. Despite their potential importance, twin networks have not been widely investigated from a machine learning perspective. We show that the graphical nature of twin networks makes them particularly amenable to deep learning.
So, how do they work? First, deep twin networks correspond to neural networks whose architecture corresponds to the graphical structure of the twin network representation of the structural causal model to be learned.Our approach has two stages: first, we train the neural network to learn the counterfactually ordered causal mechanisms that best fit the data. Then we interpret it as a twin network on which standard inference can be performed to estimate counterfactual distributions. This process is graphically depicted below.

With the flexibility and computational advantages provided by neural networks, our model can handle an arbitrary number and type of confounders while estimating counterfactual probabilities. Moreover, twin networks were designed to address the large computational resources required for abduction-action-prediction counterfactual inference. As such, deep twin networks are faster and less memory intensive than standard abduction-action-prediction, and the inference can be conducted in parallel rather than in a serial nature.
Conclusion
Discovering and understanding causal relationships is a fundamental challenge in science and machine learning. In this work, we introduced an innovative approach to learn causal mechanisms and perform counterfactual inference using deep twin networks. We demonstrated that their approach achieves accurate counterfactual estimation that aligns with domain knowledge through empirical testing on real and semisynthetic data.
For more about our findings, please refer to our paper: Estimating categorical counterfactuals via deep twin networks Athanasios Vlontzos, Bernhard Kainz & Ciarán M. Gilligan-Lee Nature Machine Intelligence, 2023



