Local Interference: Removing Interference Bias in Semi-Parametric Causal Models

Introduction and Motivation

Causal inference helps us answer “what-if” questions—what would happen if we recommended a podcast instead of an audiobook, or if we promoted one track over another? A key challenge arises when attempting to do this in the real world: interference bias. This happens when one unit’s treatment affects another’s outcome. For instance, recommending a podcast instead of an audiobook may lead to less consumption of the audiobook even though no intervention was directly applied to it.

Traditional causal inference techniques assume no interference between units, a requirement known as SUTVA (Stable Unit Treatment Value Assumption). When this assumption is broken—as it often is—our causal estimates can be way off. Past approaches have required extensive knowledge about how units interact, usually encoded in detailed graphs, as well as the requirement that there exist units not impacted by interference. These conditions are highly unlikely to be met in practice.

Our recent paper offers a simpler alternative, motivated by the following observations: 

1. Firstly, those units who are not themselves treated---that is, units that are only impacted by spillover effects from treated units—provide a sense of the level of interference present. If interference experienced by the untreated units is representative of that experienced by the treated units, then in principle one could use spillover effects on untreated units to remove, or reduce, interference bias.

2. Secondly, even in situations where the interaction graph between all units is not fully known, there are real-world settings where the problem can be simplified. Indeed, in the case of advertisements in an online marketplace for instance, a given advertisement will usually only compete with other advertisements that are relevant for the same buyer in that marketplace and not others. Hence, even when the interaction network is not fully known, certain domain knowledge about how interference is ``localised'' can make the problem tractable.

Our work shows that, by formalising the above two observations, one can remove interference bias in some semi-parametric settings.

Toy Example: The Power of Spillovers

To explain how this works in a concrete manner, let’s walk through the following simplified example. Consider three units. Units 1 and 2 are treated; unit 3 is untreated. We assume that unit 2’s treatment affects the outcomes of both units 1 and 3 in the same manner. This is graphically depicted in the causal diagram below. Because unit 3 is untreated, that is T₃ = 0, any effect we observe in its outcome must come from interference caused by unit 2’s treatment affecting unit 3’s outcome. By comparing the outcomes of units 1 and 3, we can isolate the direct effect of unit 1’s treatment by subtracting out the spillover effect on unit 3. As unit 2’s treatment impacts both unit 1 and unit 3 in the same manner here, the level of interference they experience is the same. This is what enabled us to use the spillover of unit 2’s treatment on unit 3’s outcome to remove interference on unit 1. 

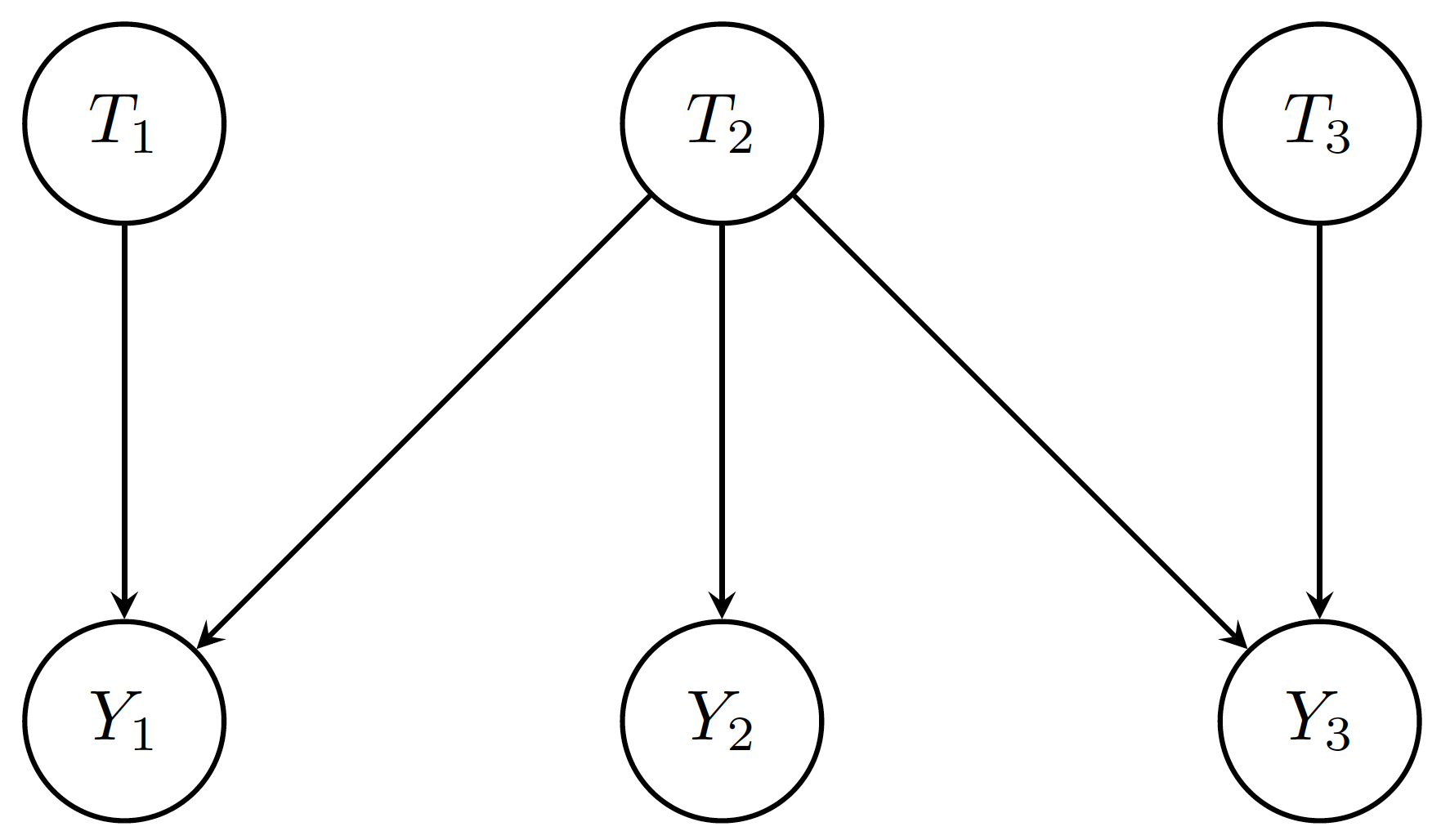
To recap, we had domain knowledge informing us that unit 1 and unit 3 experienced the same level of interference, and thus could consider the untreated unit 3 an interference ”match'' for the treated unit 1—in a similar manner to matching on confounders in propensity-based causal inference.This observation foreshadows our approach to removing interference bias

A New Framework: Interaction models with local interference

To formalize when and how interference can be accounted for, we propose a new model: Interaction Models with Local Interference.

This model assumes:

• Interference effects are captured by an interference signature, summarizing how that unit is influenced by others.

• Each unit’s outcome depends on its own treatment and covariates, as well as its interference signature.

• There’s an overlap condition: units with similar covariates and interference signatures must appear in both the treated and untreated groups. This can be thought of as an extension of the usual overlap condition for confounders in propensity-based causal inference.

Domain knowledge and feature engineering can be used to specify the interference signature for a given problem setting, in much the same way as domain knowledge and feature engineering are used to specify relevant confounders in standard causal inference applications. For example, ads in an online marketplace will only interfere with each other's outcomes—that is, compete—if they are targeting the same user cohorts. The interference signature here will be descriptions of those user cohorts. As another example, consider estimating the impact of a public policy in a city. Here the impact of similar policies in adjacent regions weighted by proximity could provide an interference signature.

The True Average Causal Effect

The ultimate goal of removing interference bias is to be able to estimate the True Average Causal Effect (TACE): what the average outcome would be if everyone were treated versus if no one were treated—with interference stripped out.

One of the main results of our paper is that in additive models interactions models with local interference—where the treatment and interference affect the outcome in separate, additive ways that are each allowed to be highly non-linear—the TACE is identifiable. We provide a formula for calculating the TACE in this setting using Inverse Probability Weighting (IPW), adjusting for both covariates and interference signatures. This is analogous to traditional methods adjusting for confounding variables, but expanded to include interference.

When the TACE cannot be identified

Our paper also proves a limitation: in non-additive models, where treatment and interference interact in more complex ways (like multiplying each other), the TACE often cannot be identified from observational data alone.

This result emphasizes that semi-parametric assumptions—especially the additive structure—are not just convenient, but necessary for identification unless additional assumptions or data are available.

That said, some alternative causal quantities (like the causal risk ratio, see our paper for full details) can still be identified under certain multiplicative models.

Testing our approach: COVID-19 in Switzerland

To test our method in practice, we applied it to real data on the spread of COVID-19 across Swiss regions, or cantons, in 2020. Cantons adopted different levels of policy strictness (e.g. mask mandates, gathering restrictions), and because people travel between regions, policies in one canton could influence outcomes in another—a clear interference setting.

We considered two types of interference signatures:

• IA: Based on the average policy status of neighboring cantons.

• ID: Weighted by distance between cantons.

And found that:

• Without adjusting for interference, estimates of the policy effects were biased.

• Adjusting for IA or ID using the IPW-style formula we derived reduced bias.

• When interference was artificially added in a semi-synthetic setup, using the correct signature fully corrected for bias. Using the wrong one helped, but didn’t remove bias completely.

This shows how properly defined interference signatures can help recover true causal effects, even in the presence of interference. We’ve also applied our method to internal problems at Spotify to understand the true impact of our promotion technology.

Final Thoughts

Our work provides a step forward in applying causal inference in real-world settings where interference is unavoidable. By focusing on local interference and defining appropriate signatures, we showed that its possible to identify true causal effects—without needing full knowledge of how every unit interacts with each other.

Our key takeaway: with smart modeling and domain knowledge, interference doesn’t have to ruin causal estimates. This opens up new opportunities for accurate causal inference in fields ranging from public policy to digital advertising. If you’re interested in reading more about the work, check out our paper!

For more information, please refer to our paper: Local Interference: Removing Interference Bias in Semi-Parametric Causal Models Michael O'Riordan, Ciarán Gilligan-Lee CLeaR - Causal Learning and Reasoning 2025