Collaborative Classification from Noisy Labels

On online platforms such as Spotify, users have access to large collections of content. Most of the time, these collections are too large for anyone to go through exhaustively. For example, on Spotify, users can access over 70 millions tracks and 2 million podcast episodes (as of April 2021). It is therefore important to organize all this content in a way that users can quickly find what is relevant to them.
Metadata describing each piece of content is often crucial to this organization. Let us consider podcast shows as an example. The language of each show is clearly an important piece of information, as users are unlikely to be interested in a show that is not in a language that they understand. If metadata (such as show language) is provided by third-parties (such as podcast producers), it is possible that some of that metadata will be incorrect or inconsistent.
This prompted us to ask the question: can we automatically identify and correct mistakes in the metadata? For example, can we automatically identify incorrect language labels associated with podcast shows? In a recent paper appearing at AISTATS 2021, we show that the answer to this question is: Yes!
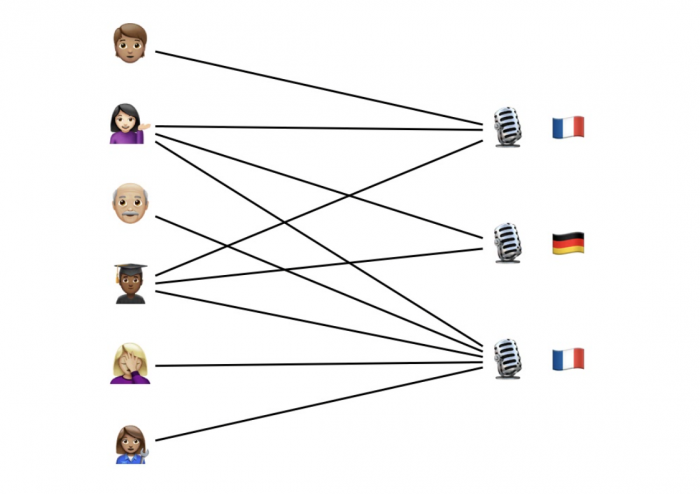
Fig 1 . The network of interactions between users and podcasts contains information that can help us correct mistakes in the metadata.
We introduce an algorithm that is simple to implement and that successfully corrects labeling mistakes across a wide range of applications. In our podcast example, we can correct almost 80% of the incorrect language labels. The key idea behind our approach is that we can take advantage of useful information contained in user-item interactions (Fig. 1). For example, it is likely that a user will only listen to shows in a language they understand. Assuming that there are not too many errors in the labels and that users typically only understand a few languages, we can identify language labels that are likely to be incorrect by reasoning based on all the user-podcast interactions we observe.
Model & Algorithm
We formalize the problem by assuming that every item (e.g., every show) belongs to one of several classes (e.g., languages), and the goal is to identify the correct class for each item. We start by postulating a probabilistic model that connects assumptions about users, about items and about interactions between users and items. Informally, our model states that
Users are characterized by the affinity they have for each class. Users are likely to have different affinities for different classes.
Items are characterized by their class. The true class of an item is likely to correspond to the provided label, but errors can happen (with some probability).
Users are likely to interact with items belonging to classes for which they have a high affinity.
A graphical representation of the model is presented in Fig. 2.
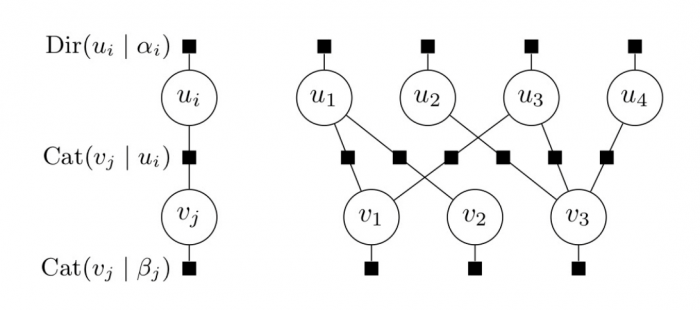
Fig 2 . Undirected graphical model. Users are represented by a distribution over classes u i with a Dirichlet prior, items a represented by single label v j with a categorical prior, and each interaction is represented by a categorical potential.
We can then identify and correct mistakes in the labels by doing probabilistic inference in the graphical model. To this end, we use a well-known algorithm called coordinate-ascent variational inference (CAVI).
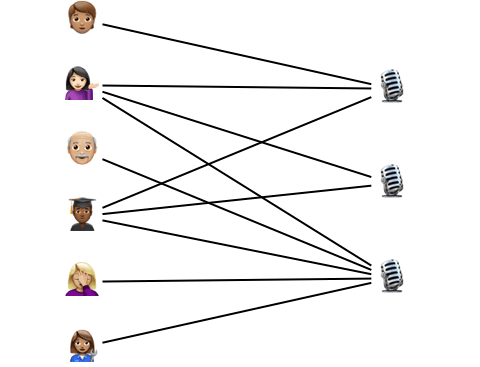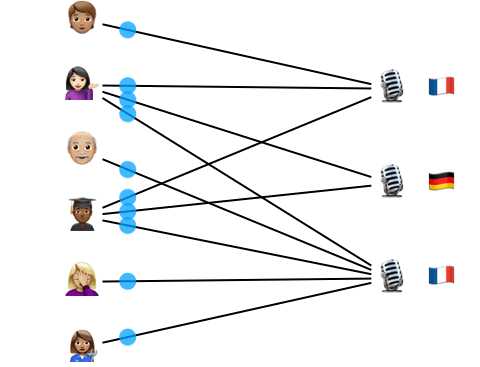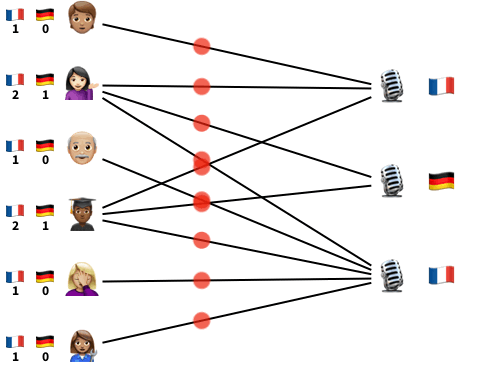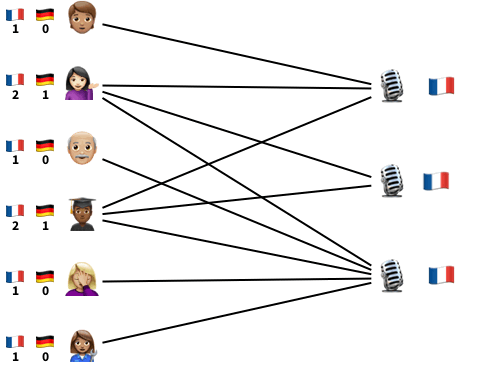
Fig 3 . Probabilistic inference helps us identify and correct mistakes in the items’ labels. The inference algorithm we use, CAVI, can be seen as passing messages along the edges of the interaction network.
Even though we use advanced ideas from approximate Bayesian inference, the resulting algorithm is very simple. It consists of repeatedly sending messages along the edges of the interaction graph and updating parameters using simple aggregations (Fig. 3). It only takes about a dozen lines of Python code, and we even successfully implemented it in SQL!
Theoretical Guarantees
In a way, our algorithm can be seen as a special-case of well-known algorithms from statistical relational learning, in particular collective classification. What sets our work apart is that we are able to analyze our algorithm theoretically and give guarantees on when it is possible (or impossible) to recover the errors.
To this end, we study a generative model of online platforms. This model resembles the one we described in the previous section: it describes how users’ affinities are distributed, how item classes are distributed, and how errors arise. Importantly, it also describes how users decide which items they interact with: under our generative model, users first sample a class, then pick an item within this class uniformly at random.
The parameters that describe the generative model include:
the number of items N,
the number of users M,
the number of interactions per user S, and
the error probability δ.
We focus on a setting where N tends to infinity, M is a function of N, and the other parameters are fixed. We consider the probability P(perfect recovery) that our algorithm successfully identifies and corrects all errors. We are able to show the following results (stated here informally).
If M > C2 N log N, then P(perfect recovery) → 1 as N → ∞ using our algorithm
If M < C1 N log N, then P(perfect recovery) → 0 as N → ∞, for any algorithm.
The take-away is that, under the idealized generative model we consider, our algorithm is order-optimal: it can recover all errors essentially as soon as possible. Since we fix the number of interactions per user, the threshold on M coincides (up to constant factors) with the critical number of edges needed to make sure the interaction graph is connected.
Experimental results
That sounds great, I hear you say, but how well does it work in practice? When we evaluate our algorithm on the podcast language labeling task we have used as a running example (where the labels range over 40 different languages), we manage to identify and correct 80% of the errors present in the data (Fig. 4). This is significantly better than competing approaches proposed in the literature.
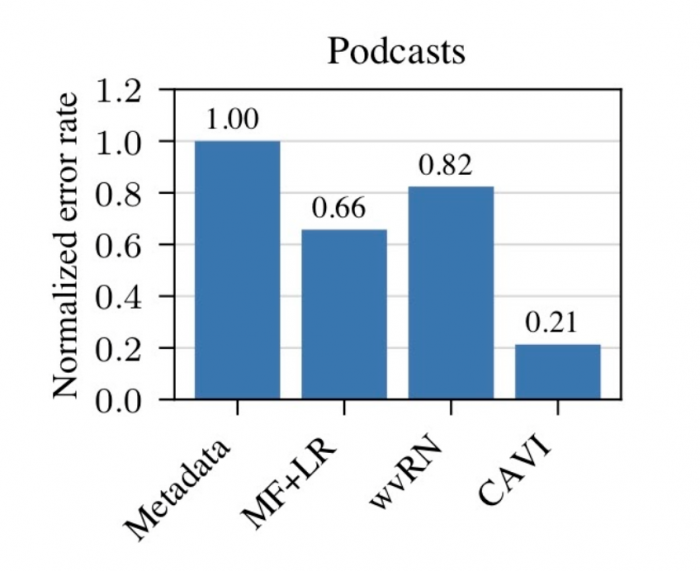
Fig 4 . Our algorithm (CAVI) corrects 80% of the errors on a dataset of podcast language labels (the baseline error rate is normalized for confidentiality).
We also test our methodology on other applications: tagging questions on a Q&A platform, categorizing products on an e-commerce website, and locating restaurants on a review website. In addition, we run experiments where we control the amount of noise we inject into the labels (i.e., the corruption rate). It turns out that we can corrupt well over half of the labels before our approach breaks down (Fig. 5).
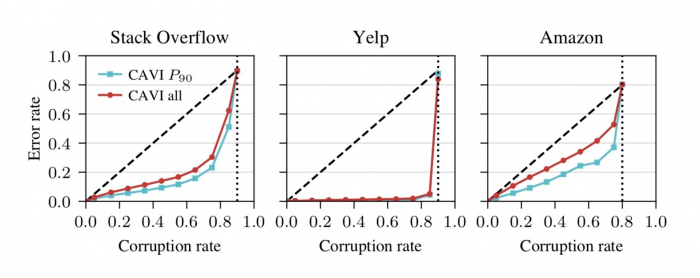
Fig 5 . Performance of our algorithm as a function of the amount of noise in the label tested on three different datasets.
Conclusion
Taken together, our results show that a simple idea—taking advantage of user-item interactions—leads to an effective algorithm that identifies and corrects noisy labels. In our paper, we discuss interesting connections to collective classification, collaborative filtering, error correcting codes, topic models, and more.
Find out more in our paper “Collaborative Classification from Noisy Labels” published at AISTATS 2021, and check out our codebase if you are interested in trying it out on your own data.



