Optimizing for the Long-Term Without Delay

July 24, 2023 Published by Thomas M. McDonald, Lucas Maystre, Mounia Lalmas, Daniel Russo, Kamil Ciosek

TL;DR: On online platforms such as Spotify, recommender systems are increasingly tasked with improving users’ long-term satisfaction. In practice, this means training these systems to explicitly optimize for long-term notions of success, such as repeat engagement or retention. This leads to a particularly challenging cold-start problem: when a new piece of content appears, it might take weeks or months to understand the long-term impact of recommending that item to users. In a new paper that we are presenting at the KDD 2023 conference, we argue that there is an effective way to address this problem, by making use of intermediate outcomes observed between making a recommendation and fully observing the long-term metric of interest.

Recommender Systems and Long-Term Goals

Recommender systems are instrumental to the success of online platforms like Spotify: they help users find new, relevant content among millions of items. Traditionally, most recommender systems are trained to optimize short-term notions of success: outcomes like clicks, or streams, or perhaps the length of a session. The underlying belief is that driving these outcomes helps us achieve higher-level goals such as increasing users’ satisfaction, retaining users on the platform, and so on. In practice, this approach has been very effective. But it only works up to a point: short-term proxies fail to capture all the nuances of successful recommendations, and how they relate to long-term user satisfaction goals.

To overcome the limitations of optimizing for short-term proxies, there has been an increasing interest in optimizing recommender systems explicitly for long-term outcomes. This can be extremely successful: At Spotify, we have developed a podcast recommender system that optimizes recommendations for long-term success [1], and shown that it can lead to large increases in long-term engagement. The key is to explicitly estimate and target based on long-term outcomes, by collecting data about the long-term outcomes associated with past recommendations. In that specific application, we estimate the number of days a user is likely to engage with a new show that they discover through a recommendation over a 2-month period.

While this approach holds a lot of promise, it exacerbates a challenge that all recommender systems have to face, the so-called item cold-start problem. The challenge is as follows: when a new piece of content is released, we need to learn how to recommend it. If the outcomes we use to learn about and adjust recommendations are only observed after a long delay (2 months in our podcast recommendation example), then at first sight it seems that there is no way other than to wait for a long time to get data about the impact of recommending that content. As such, in the context of this cold-start problem, we see that there is an apparent tradeoff between alignment and velocity:

• Short-term proxies enable recommender systems to quickly learn about new content, but they might be poorly aligned with long-term success, as we discussed.
• Long-term signals are better aligned, but are only available after a long delay (by construction!), making it difficult to learn how to recommend new content.

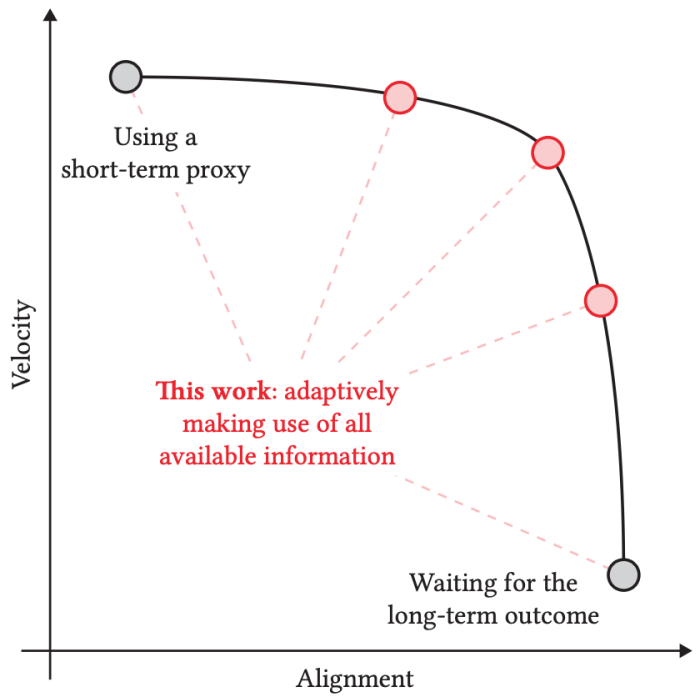
In this work, we show that this tradeoff can be circumvented, and that we do not need to give up on optimizing for the long-term: when new content appears, we can do much better than naively waiting for long-term outcomes of interest to be fully available. The key intuition is that, as soon as a recommendation is made, we can start guessing what the long-term impact will be. Every day brings a little bit of information that lets us refine our guess. These guesses can be used to drive recommendations, and we give evidence that doing so can be very effective in practice.

To study the item cold-start problem in a rigorous way, we frame it as a content exploration task. Starting with a set of content which we know nothing about, we need to make a sequence of recommendations. We take the terminology of reinforcement learning: each recommendation results in a certain amount of reward, quantifying the long-term success of the recommendation. This reward is only observed after a long delay. The goal is to minimize the cumulative regret, i.e., the difference between the sum of the rewards obtained over successive rounds and the theoretical optimum assuming full knowledge. To this end, the recommendation agent needs to explore the space of actions, but also quickly identify promising actions in order to exploit them.

Making Use of Intermediate Observations

The idea that is at the core of our approach is as follows. Even though the reward associated with a recommendation is only observed after a long delay, we might be able to observe intermediate outcomes, earlier on, that are correlated with the reward. This is pretty clear in our podcast application: if the reward is the number of days a user engaged with a podcast show they discovered through our recommendation over 60 days, then every single day that passes after we make the recommendation brings a little bit of information about the final long-term reward. Taking this to the extreme: after 59 days, we should have a pretty good idea about the number of days a user engages with the show over the full 60 days.

We formalize this by assuming that the reward corresponding to a recommendation, denoted by r, is a weighted combination of intermediate outcomes, denoted by z₁, …, z_K, observed after increasing delays Δ₁ ≤ … ≤ Δ_K.

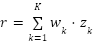
We call (z₁, …, z_K) the trace. To simplify things, we consider a non-contextual setting, where we do not seek to personalize recommendations. In that case, all we need to learn about is the expected reward; that is, we integrate out the randomness due to different users’ response to a recommendation. Instead of reasoning about the expected reward directly, we instead reason about the expected trace, i.e., the expected value of (z₁, …, z_K).

A key component we develop in our paper is a predictive model of the reward. This reward model is trained to make predictions about the expected trace (and thus, the expected reward) from a dataset consisting of full and partial traces. The crux is that partial traces (i.e., traces for which we have only observed the first few elements; say the first 5 days of engagement in our podcast example) can be very informative and help us make accurate predictions. We discuss this reward model in details in our paper, but we briefly highlight two important aspects:

1. For each action, we instantiate a Bayesian filter as our reward model. The Bayesian framework lets us reason about the uncertainty over our estimate, as we observe increasingly more information (more traces, and more intermediate outcomes for each partial trace). In short, we progressively refine a Gaussian belief over the mean trace by folding in information as it arrives.
2. To train the parameters of the Bayesian filter, we take advantage of historical data on similar but distinct actions we have observed in the past. For example, we use full traces from previous content releases. The hypothesis is that correlations between intermediate outcomes and the long-term reward remain stable over time. This turns out to work well, and is an important feature of our approach.

In the context of habitual podcast engagement, we observe that there are strong correlations between users’ engagement in the first few days and their cumulative engagement over 60 days.

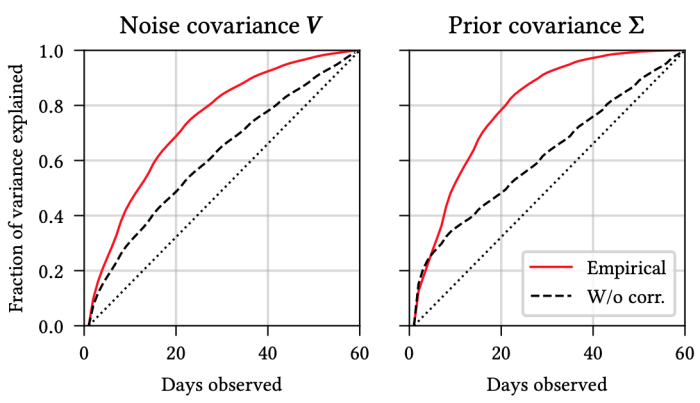
This means that we can start making fairly accurate inferences about the 60-day reward after observing just 10-20 days of data. Another perspective on this is given by the following figure, which displays the predictive performance as a function of (a) the number of traces and (b) the number of intermediate outcomes observed in each trace.

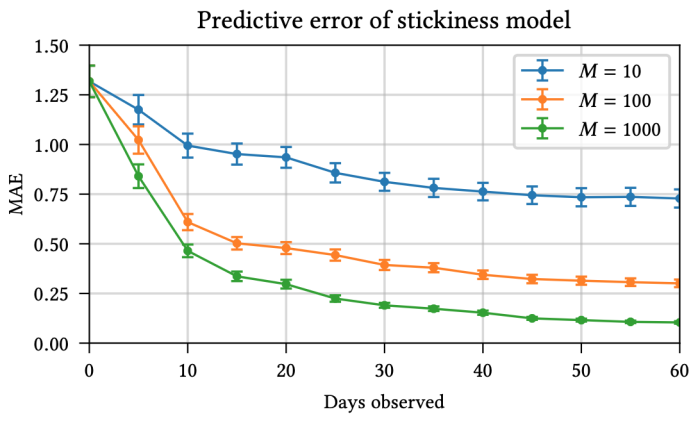
Again, we see that just observing the first few days enables reasonably accurate predictions about the mean long-term reward.

The Impatient Bandit

The reward model, by itself, does not tell us how to make recommendation decisions. To select actions at each round, we combine the reward model with an algorithm named Thompson sampling. Informally, Thompson sampling selects actions randomly at each round, but with a bias towards actions that have either high expected reward, or high uncertainty (as per the reward model). This bias enables us to navigate the exploration-exploitation trade-off effectively. At first, actions are chosen randomly, but progressively the algorithm converges on actions that show the biggest promise.

We illustrate this on our podcast recommendation application. We compare variants of Thompson sampling with four different reward models. Starting with a pool of 200 different podcast shows (actions), we run hundreds of simulations and plot the average regret as well as the entropy of the empirical distribution over actions as time progresses.

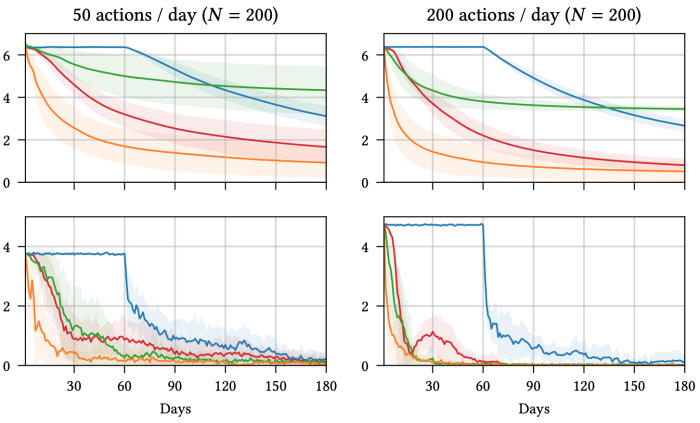
Focusing on the regret plots (top row), we can make the following observations.

• The blue lines represent a naive baseline that waits the full 60-days before updating its belief about the long-term reward. Clearly, the feedback loop is too slow: it takes way too long before outcomes of early recommendations start guiding future recommendations.
• The green lines represent the performance we might expect when using a short-term proxy. Because of the shorter feedback loop, the system starts learning almost immediately. But because short-term success and long-term success are not perfectly aligned, in the long run we fail to find the best actions (as evidenced by the regret not going to zero).
• The orange lines represent the performance of an imaginary “oracle” system, where the full 60-day reward is observed straightaway, without any delay. This is impossible in practice, but it is still useful to check, as it provides a bound on the performance that any system would be able to achieve.
• Finally, the red lines represent our approach, which relies on progressively-revealed intermediate outcomes. We see that it improves significantly on the blue and green lines. It is striking to observe that the red line is much closer to the orange line than to the blue one.

In conclusion, by making good use of intermediate outcomes, we can do almost as well as if the long-term reward was revealed immediately, without delay!

For more information, please refer to our paper:
Impatient Bandits: Optimizing for the Long-Term Without Delay
Thomas McDonald, Lucas Maystre, Mounia Lalmas, Daniel Russo, and Kamil Ciosek
KDD 2023

References:
[1] Optimizing Audio Recommendations for the Long-Term: A Reinforcement Learning Perspective.
Lucas Maystre, Daniel Russo, and Yu Zhao.
Presented at the Reinforcement Learning for Real Life Workshop @ NeurIPS 2022 (available on arXiv)